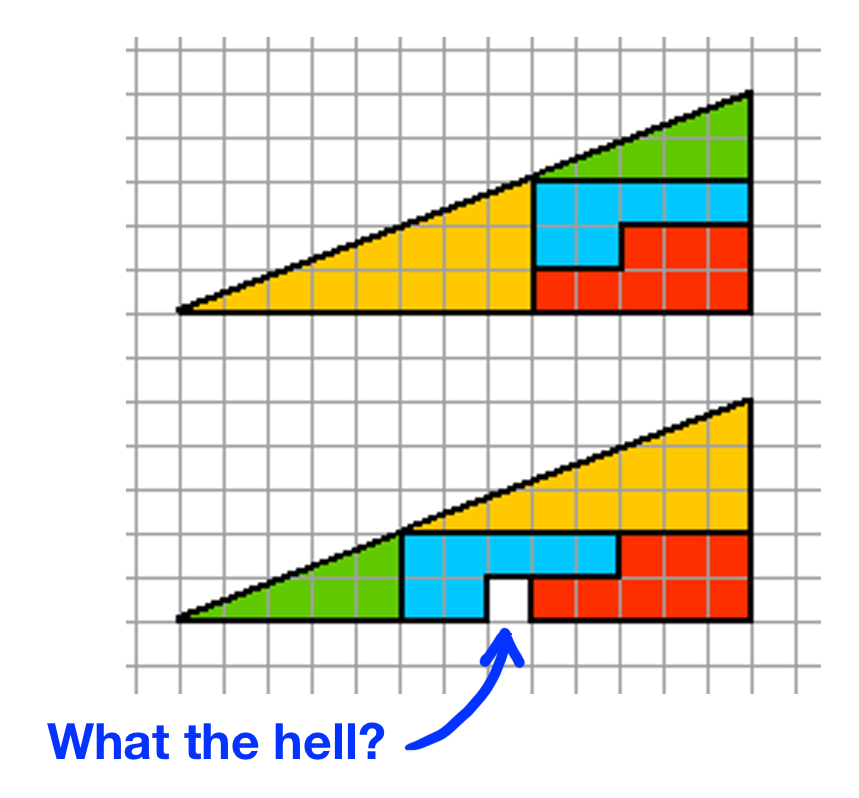
The Confusing Triangle Situation

Welcome to the confusing triangle situation. What the hell?

The same four shapes, when rearranged, seem to take up less space and leave a blank square. How is that possible?

[expand title=”SOLUTION“]

A friend sent this to me in college and it ruined my life for a little before it finally clicked. Here’s what’s happening:

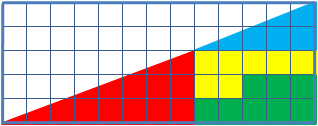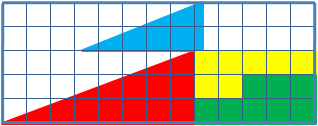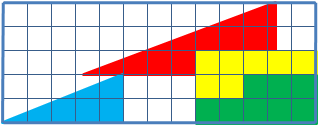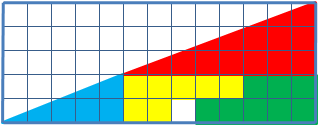
So it seems like all that’s happening is a rearrangement of the pieces of a single big triangle:1

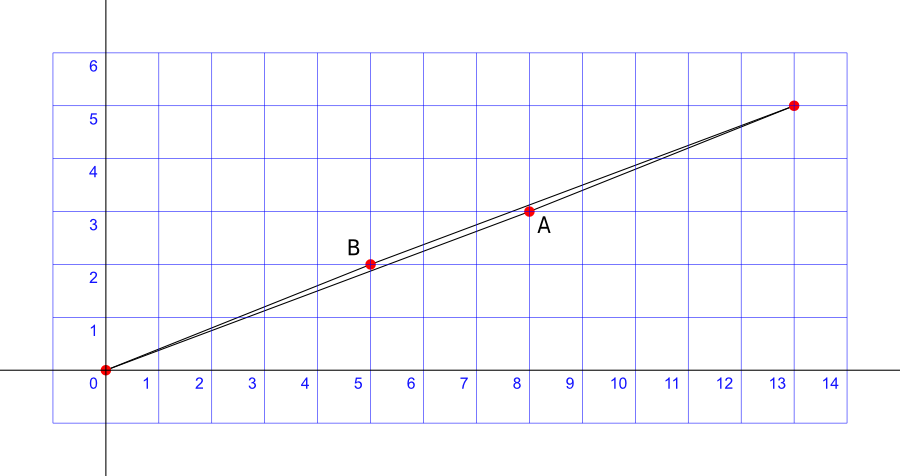
But something tricky is going on with the big hypotenuse in both triangles.

It’s all about slope. The blue triangle, red triangle, and what appears to be the large triangle all have different slopes.

Blue triangle hypotenuse = slope of 2/5 = 16/40

Red triangle hypotenuse = slope of 3/8 = 15/40

Big triangle hypotenuse = slope of 5/13 = 15/39 = (15.38)/40

Those three slopes are close enough that they can appear identical in a drawing (especially one with thick outline lines)—but the big hypotenuse is actually not a straight line, but a two-line angle in the shape of a really wide V.2

In the top triangle, the V goes “in”—so there’s no room for extra space (hypotenuse A). In the bottom triangle, the V goes “out” (hypotenuse B)—clearing up space for one extra square. The little slit of area inside the two hypotenuses in the above diagram is the same as the area in one square on the graph.

[/expand]

_______

If you like Wait But Why, sign up for our email list and we’ll send you new posts when they come out.

To support Wait But Why, visit our Patreon page.

___________

More puzzles on Wait But Why:

The Stick Figure puzzle

The Three Jellybean Problem

The Puzzle of the Pirate Booty

The Two Envelopes Problem

The Infinite Checkerboard Quandary

And one very big puzzle: