Welcome to Mini Week, a week where I’m writing a new mini-post for each weekday. Good idea? Terrible idea? I’m not sure. But based on feedback and whether or not doing five posts in a week makes me die, it can be a one-time thing or something that happens again. Either way, off we go.
___________
You’re wandering through a faraway land one day when you pass a plum tree. Excited, you pick a plum from the tree, but just as you’re about to take your first bite, you’re confronted by a nearby man.
“You stole one of my plums,” he says.
You try to give the plum back and explain that you didn’t mean to steal from him, you just really like plums so you picked one.
“Those aren’t mutually exclusive,” he says. “It sounds like you both really like plums and meant to steal one from me.”
“I guess, yeah, but like…” you say.
“The penalty for stealing plums in our faraway land is death,” he says.
“Shit,” you say.
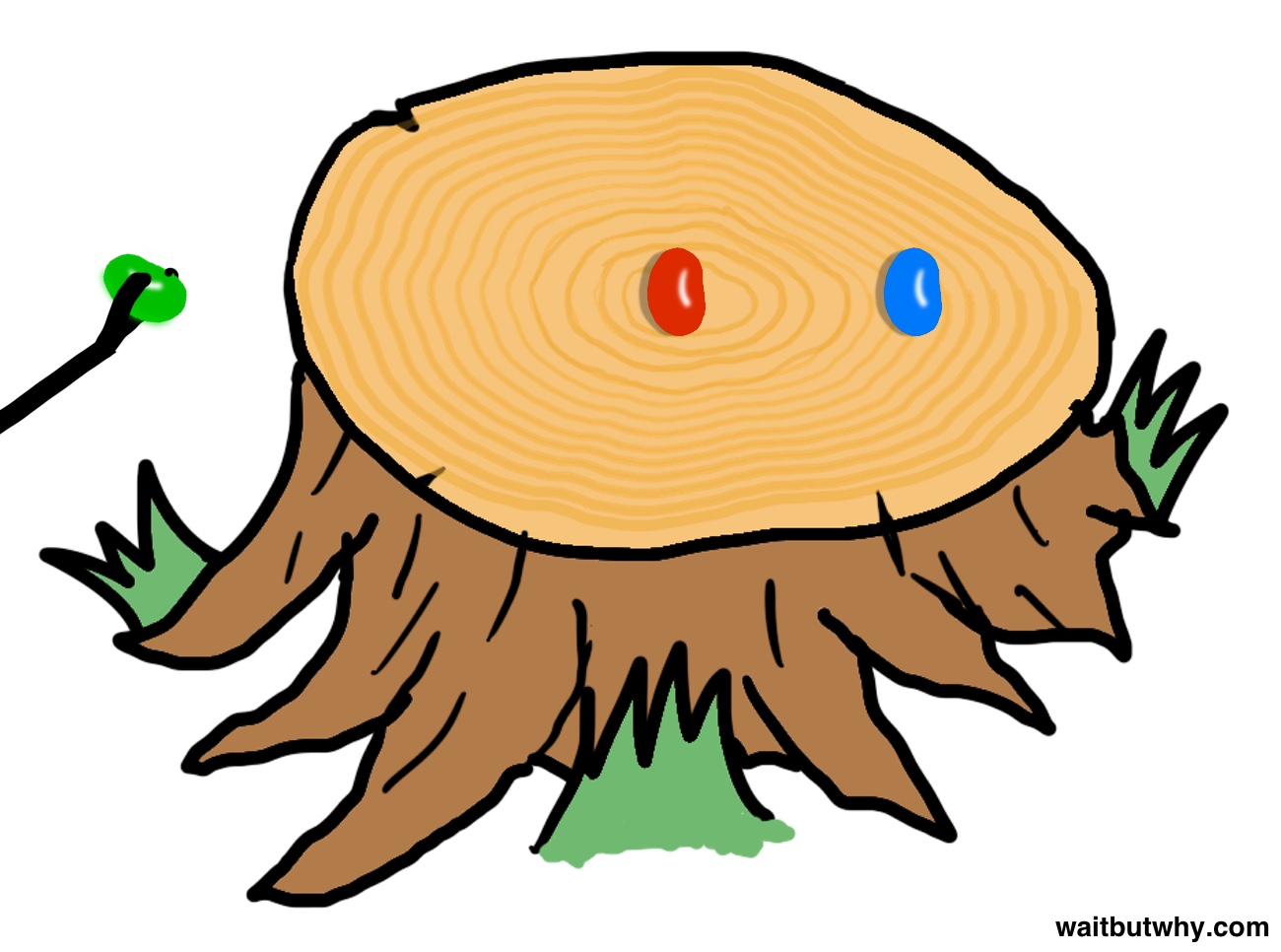
He takes you with him over to a tree stump and asks you to sit down next to the stump. He reaches in his pocket and takes out three jelly beans—a green one, a red one, and a blue one. He sits down on the other side of the stump and puts the three jelly beans on the stump in a row.
He says, “Here’s some good news. The way we do the death penalty here is that you have a chance to get out of it. Here’s the deal: Two of the jelly beans on the stump are poisonous—you’ll die within 30 seconds of eating either one of them. But one of the jelly beans isn’t poisonous and won’t harm you at all. All three of the jelly beans are delicious. The situation works like this: You pick one of the jelly beans and eat it, and if you happen to pick the non-poisonous one, you’re free to go. Cool?”
“Cool,” you say. He tells you it’s time to choose a jelly bean.
You choose the green one.
Before you put it in your mouth, the man stops you and says, “Wait a minute—there’s one other little tradition we have that we do with each prisoner. Hold on to your jelly bean. I’m going to remove one of the other two jelly beans and put it back in my pocket, and I’m going to remove a poisonous one. I know which colors are poisonous and which aren’t, and one thing I can tell you is that blue jelly beans are poisonous.”
He takes the blue jelly bean and puts it back in his pocket. That leaves the red jelly bean still on the stump and the green jelly bean still in your hand.
“Okay, time to eat your jelly bean,” he says. “Oh and we also always allow prisoners to change their mind up until the last second, so if you want to switch to the red one, you can. I don’t care. But you need to eat one of them in the next 10 seconds.”
So the question is—which jelly bean do you eat? Does it even matter?
Stop and think about what you’d do in this situation before moving on.
___________
Here’s the weird thing about that question—yes, it matters. It matters a lot. Knowing only what you know in that situation, there is one clear choice: the red jelly bean.
My guess is that when you thought about it, you decided to stick with your original decision and eat the green one. Because with two jelly beans left, you had a 50/50 shot, and it feels better to stick with your original choice than to switch. Right?
Wrong. Very wrong.
The green jelly bean is double as likely to kill you as the red jelly bean. Here’s why:
When you initially picked the green jelly bean, there was a 1/3 chance that it was the safe one to eat, and a 2/3 chance that it was poisonous and the safe one was still on the stump. When the man removed a poisonous blue jelly bean from the stump, it told you no new info about the green jelly bean in your hand—that still had a 1/3 chance of being safe. But removing the blue jelly bean told you a lot about the red jelly bean—it told you that if the safe jelly bean had been on the stump, the red one is safe.
Put another way, if you picked a poisonous jelly bean—which you would do two-thirds of the time—then choosing to switch after he removes one will save you every time. If you picked the safe one to start off with—which happens one-third of the time—then switching will kill you. So switching is a good choice two-thirds of the time.
You could run a pretty quick simulation: If you ran this process 300 times and picked the green jelly bean each time, about 100 of the times, it would be safe to eat and switching to the red bean would kill you. The other 200 or so times, the green jelly bean would be poisonous and switching to the red bean would save you.
One other way to look at it is this—say instead of three jelly beans, the guy puts down 1,000 jelly beans and tells you again that only one is safe. So this time, instead of two poisonous jelly beans to contend with, there are 999. He labels them each with a number, 1-1,000, and asks you to choose. You choose jelly bean 267 and hold it in your hand, leaving 999 jelly beans on the stump. Then, while you hold onto jelly bean 267, the man removes 998 jelly beans from the stump and tells you that all 998 of them are poisonous. All that’s left on the stump is jelly bean 749. He tells you you can stick with jelly bean 267 or switch to jelly bean 749—what would you do?
You’d switch. Jelly bean 267 has a 1/1,000 chance of being safe. There’s nothing special about it. You picked it and it sat on the sidelines as 998 poisonous jelly beans were removed from the 999 on the stump. Jelly bean 749 is special—it’s the survivor. There’s a tiny, 1/1,000 chance that you happened to pick the non-poisonous jelly bean, and if that’s the case, then the man just took 998 jelly beans at random from 999 that were all poisonous. But far more likely is that the jelly bean you picked is one of the poisonous ones, meaning the stump only has 998 poisonous jelly beans on it. So when the man says he’s going to take 998 poisonous ones off the stump, he has no choice—he has to leave the safe one there, so jelly bean 749 is left there very intentionally. Jelly bean 749 is the one you want to eat—it’s been through the tough test and survived, while the one in your hand survived nothing and is super dangerous to eat.
Back to our three jelly bean situation. Same deal. The green jelly bean in your hand and its 1/3 odds of being safe were kept in isolation during the jelly bean removal process, so the 1/3 odds are still valid. But the red jelly bean survived the removal process and all the safe choices that might have been on the stump are now consolidated into the red jelly bean. That’s why you switch.
___________
As many of you have figured out, I didn’t make this up. Well, I made the jelly bean story up—but it’s just my own version of the famous Monty Hall problem, which was popularized by Marilyn vos Savant in her Ask Marilyn column in 1990.
Monty Hall was the host of the game show Let’s Make a Deal, and one of the games went like this:
There are three doors, labeled 1, 2, and 3.
Behind one of them is a new car. Behind each of the other two is a goat. You get to pick a door, and if you pick the door with the car behind it, you win the car.1
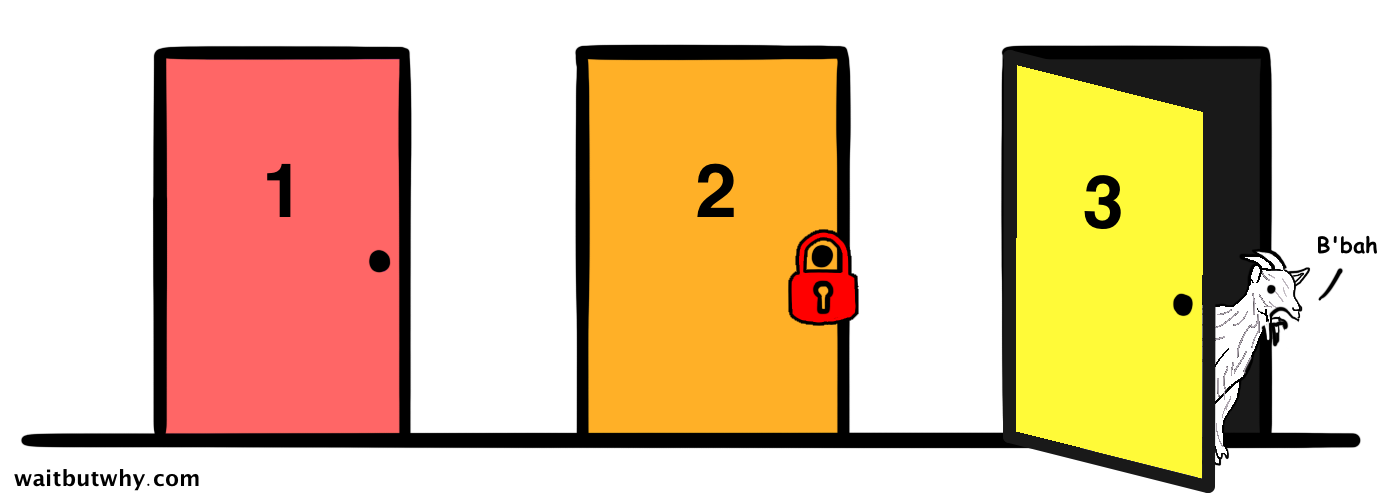
You pick Door 2, but before you have a chance to open the door, Monty, who knows which door contains the car, tells you he’s going to release a goat from behind one of the two doors you didn’t pick. He opens Door 3 and a goat comes running out.
He then gives you an option to switch from your original choice before opening a door.
Marilyn explained the problem and then explained why it was definitely the right choice to switch to Door 1—because if you were wrong in your original choice of Door 2, then the car will be behind Door 1. And there’s a 2/3 chance that you were wrong.
But over the next week, Marilyn received over 10,000 letters, including over 1,000 from PhD’s—and almost all of the letters were berating her for her huge mistake. One PhD put it like this:1
“You blew it, and you blew it big! Since you seem to have difficulty grasping the basic principle at work here, I’ll explain. After the host reveals a goat, you now have a one-in-two chance of being correct. Whether you change your selection or not, the odds are the same. There is enough mathematical illiteracy in this country, and we don’t need the world’s highest IQ propagating more. Shame!”
When people first hear the Monty Hall three-doors problem (or the Tim Urban inane jelly bean story), it doesn’t matter how smart they are—they almost always get it wrong and fervently believe that the final two options have an equal probability of being correct. Which is why almost everyone chooses not to switch their decision when given the opportunity.
One note is that this problem only works with three key conditions in place:
1) The host must always open a door, and it has to be one that was not picked by the contestant.
2) The host must know where the car is and always open a door with a goat behind it.
3) The host will always give you the option to switch your choice.
If any of those conditions isn’t there, the problem doesn’t work. For example, if the host doesn’t know where the car is and takes a guess by opening one of the other two doors, and a goat runs out, then it’s no longer better to switch your choice—it’s 50/50.2
A third version of this problem is the Three Prisoners problem, which I’ll explain in this footnote3 for those who are interested.
So—
Has it clicked? You with me? Or still in 50/50 land?
___________
If you liked this, you’ll probably like these other Wait But Why posts:
What could you buy with $241 trillion? – among other things, a pizza the size of Niger.
7.3 billion people, one building – super tight squeeze.
Graham’s Number: The biggest shit ever – seriously though.
_______
If you like Wait But Why, sign up for our email list and we’ll send you new posts when they come out.
To support Wait But Why, visit our Patreon page.
Which for most people, is the best outcome.↩
A lot of people have asked for clarification about this. It becomes 50/50 when the host doesn’t know where the car is because now there’s a chance he also picks the car. So that creates three scenarios:
Scenario A: 1/3 of the time, you pick the car, the ignorant host reveals a goat, and switching is bad.
Scenario B: 1/3 of the time, you pick a goat, the ignorant host reveals the other goat, and switching is good.
Scenario C:1/3 of the time, you pick a goat, the ignorant host reveals the car, and the game is voided.So of the times when the host opens a door to reveal a goat (Scenarios A and B), half the time, switching is good, and half the time, it’s bad. 50/50.
When the host is NOT ignorant and knows where the car is, all instances in Scenarios B and C are consolidated into Scenario B. So now it’s:
Scenario A: 1/3 of the time, you pick the car, the host reveals a goat, and switching is bad.
Scenario B: 2/3 of the time, you pick a goat, the host reveals a goat, and switching is good.A knowledgeable host acting on his knowledge gives you more information. An ignorant host taking a wild guess gives you no new information.↩
Here’s how it goes: There are three prisoners in three separate cells—A, B, and C—and all are sentenced to death. But the king, because he’s in a good mood, has selected one of them to be pardoned. The prison guard knows who the king has selected, but the prisoners don’t. When the guard walks by Prisoner A’s cell, Prisoner A stops him and says, “I know you’re not allowed to tell me if I’m pardoned or not, but please give me something. All I ask is that you tell me one of the other two guys who is being executed. If Prisoner B is being pardoned, tell me that Prisoner C is being executed. If Prisoner C is being pardoned, tell me that Prisoner B is being executed. If I’m being pardoned, pick one of the other two at random and tell me they’re being executed.” The guard decides to grant his wish and tells him that Prisoner B is being executed. Prisoner A is pumped, thinking that he now has a 50% chance of survival—but he doesn’t. He has the same 1/3 chance of survival—what’s changed is that Prisoner C now has a 2/3 chance of survival.↩