Pre-post note to people wondering where the fuck I am:
Hi! I miss you. I’ve been working on a massive post so massive it’s hard to even call it a post. I really am nearing the end of the process, but as people who follow Wait But Why closely are aware, I’m incredibly awful at giving time predictions, so I’m going to just leave it at that.
I can’t wait to share what I’ve spent most of the last couple of years thinking about. Especially because a blogger flow is usually like this:
But the last couple years, aside from a few breaks to post something, has been more like this:
It’s been unpleasant. And I miss you. And I’ll see you back here soon.
For now, I had to briefly emerge from my hole so we can discuss Jeopardy.
___________
Like many of you I presume, I recently became obsessed with James Holzhauer’s run on Jeopardy. James is odd. He makes a lot of faces like this:

And this: But he’s weirdly likable, ridiculously impressive, and the more time that went on, the more I found myself rooting for him like a sports team. When he’d be down in Double Jeopardy, I’d be on the edge of my seat saying, “come on James!” When he’d hit a Daily Double, I’d breathe a sigh of relief. And whenever he got to Final Jeopardy needing to get the answer right to keep the streak going, I’d pump my fist like a psycho when his answer came up correct.
But he’s weirdly likable, ridiculously impressive, and the more time that went on, the more I found myself rooting for him like a sports team. When he’d be down in Double Jeopardy, I’d be on the edge of my seat saying, “come on James!” When he’d hit a Daily Double, I’d breathe a sigh of relief. And whenever he got to Final Jeopardy needing to get the answer right to keep the streak going, I’d pump my fist like a psycho when his answer came up correct.
Then, on Monday, he dashed my dreams and broke my heart—one win shy of breaking the all-time money record. Excruciating.
James was really, really good at Jeopardy. Before James went on, the show’s single-game money record was $77,000.1 That was the best anyone had ever done in 55 years of the show. James not only won 32 straight games (the second most after Ken Jennings’s absurd 74-game run), his average winning total during the run was higher than the previous $77,000 record. He now holds each of the 16 top spots on the “highest single-day Jeopardy scores ever” list.
It’s just fun watching someone be so much better than everyone else at something. It’s the same reason I like watching professional sports. Watching James on Jeopardy was like watching Steph Curry shooting threes—except in this case, the deal was that the first time Curry had one bad game, he’d be banned from the game forever and you’d never get to watch him play again.
In the aftermath of James’s one bad game, there’s been a lot of discussion about his Final Jeopardy bet, and this is the exact kind of thing I need to discuss with you, so here are my thoughts:
(For the unacquainted: Final Jeopardy is the last round of the game, and it’s only one question. After being told only the general topic category, players can wager any amount of their accumulated totals on the question. The player with the most money after Final Jeopardy is the winner, keeps their winnings, and moves on to the next day. The other two win a token $2,000 (second place) and $1,000 (third place) and that’s that for them.)
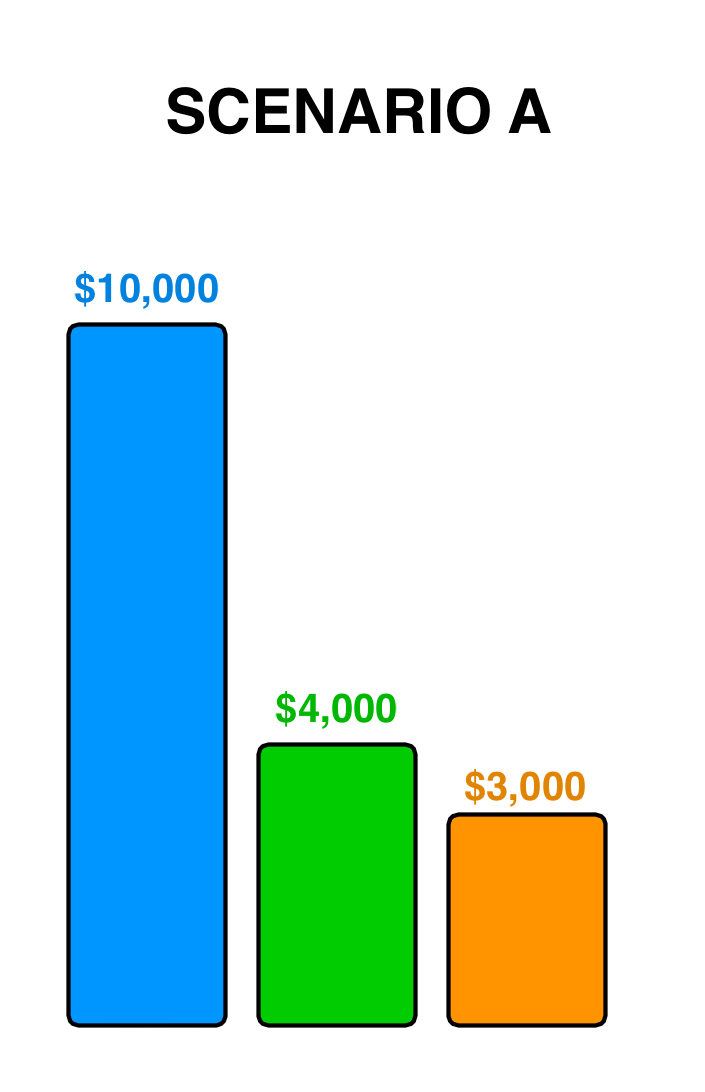
If you’re a contestant, the simplest Final Jeopardy situation is when the first-place contestant goes into the round with more than double the total that second place has. Let’s call it Scenario A.
If you’re in first place in Scenario A, all you do is calculate double what second place has and that becomes your “do not cross under any circumstances” line.
Assuming you give yourself a higher than 50% chance of getting the question right, you want to do the highest bet possible without crossing that line (so that if you get it right, you end up with the most money). So in the situation above, you’d bet $1,999. Worst-case scenario (you get it wrong, second place gets it right), you win by $1.
If you’re in second place in Scenario A, you’re out of the running for first, so no one cares what you do. Have a nice time.
James is so good that he was almost always in Scenario A situations when Final Jeopardy started, in first place, with more than (usually well more than) double the next highest total. On those episodes, Final Jeopardy was a chill situation with no stakes, other than seeing how big James’s total would be for that day.
Then there’s Scenario B. Here, second place has more than half—but less than two-thirds—of what first place has. Like this:
If you’re in first place in Scenario B, you want to make sure that if you get the Final Jeopardy question correct, you guarantee yourself the victory. So you’d assume the worst-case scenario: second place gets it right and wagers everything. That total becomes your “must cross if I get it right” line. In the above situation, that line is at $12,000. So you’d bet no less than $2,001.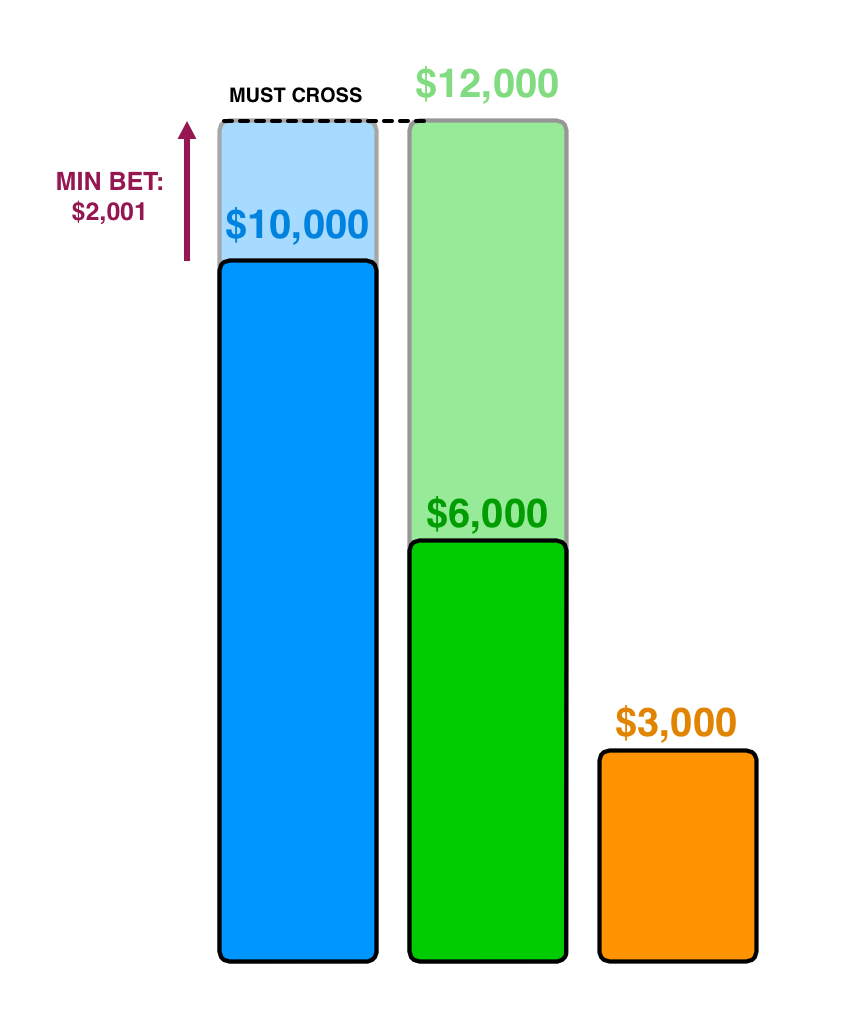 You’d also want to make sure you win in the case that you and second place both get it wrong. The worst-case scenario here is that second place gets it wrong but, for some odd reason, bets nothing. That makes their pre-round total ($6,000 in our example) your “do not cross under any circumstances” line. So your maximum bet would be $3,999.
You’d also want to make sure you win in the case that you and second place both get it wrong. The worst-case scenario here is that second place gets it wrong but, for some odd reason, bets nothing. That makes their pre-round total ($6,000 in our example) your “do not cross under any circumstances” line. So your maximum bet would be $3,999.
Assuming you don’t hate the question category, the presumption that you have a better-than-50% chance of getting the question right holds, and the rational bet would be the maximum of this range: $3,999.
Assuming first place plays optimally and stays within this range, second place in Scenario B has an easy calculation too. If first place gets it right, it’s over. If you get it wrong, it’s over. Your only chance is if you get it right and first place doesn’t. Since the only scenario in which your bet even matters is when you get it right, and you want to end up with the highest possible total in that situation, you bet everything you’ve got.2
So far, this has been non-controversial. It’s in our final scenario—Scenario C—that things get complicated.
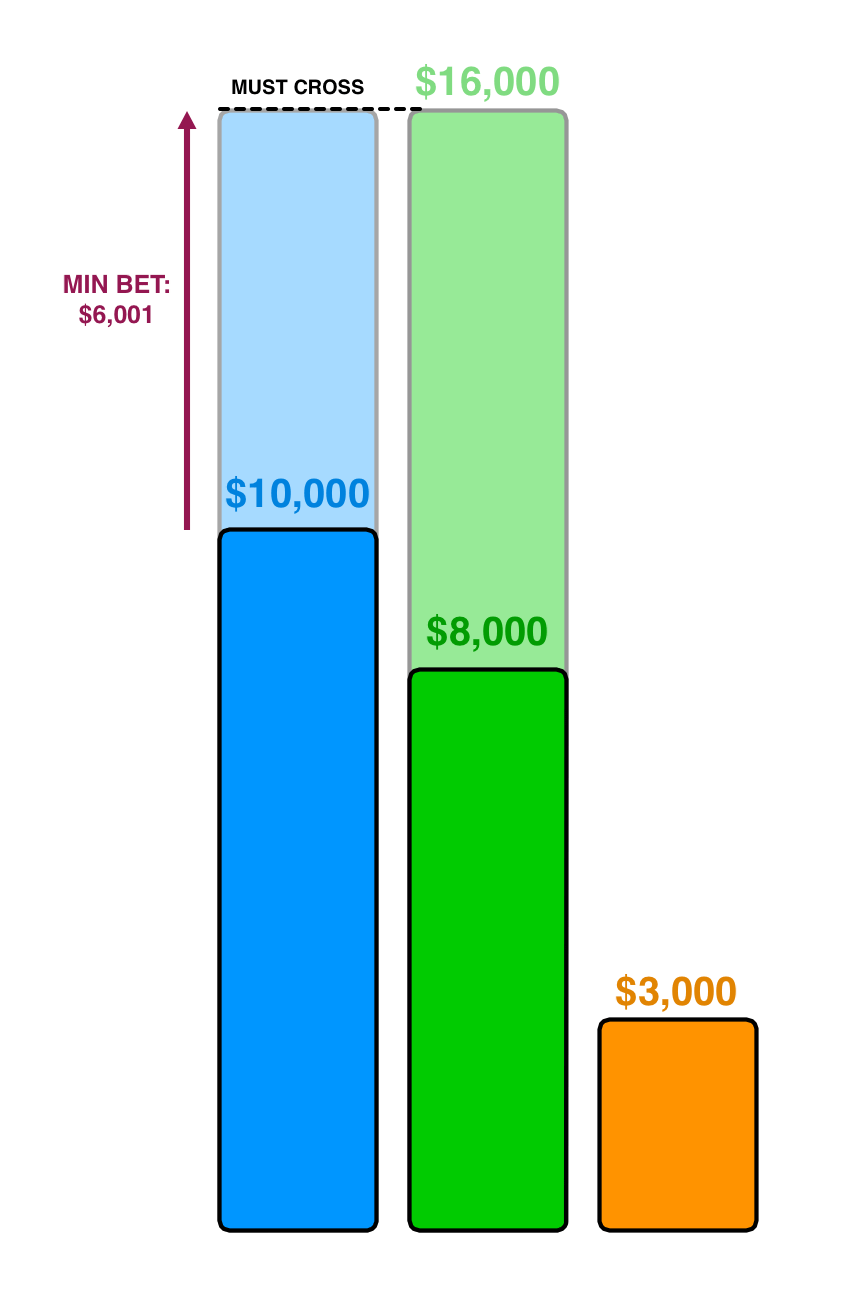
In Scenario C, second place has more than two-thirds of what first place has:
The traditional thinking is that first place wants to guarantee themselves victory in the case that they get Final Jeopardy correct, so they’d have a similar calculus to Scenario B. Here, their “must cross” line would be at $16,000, so they’d bet at least $6,001.
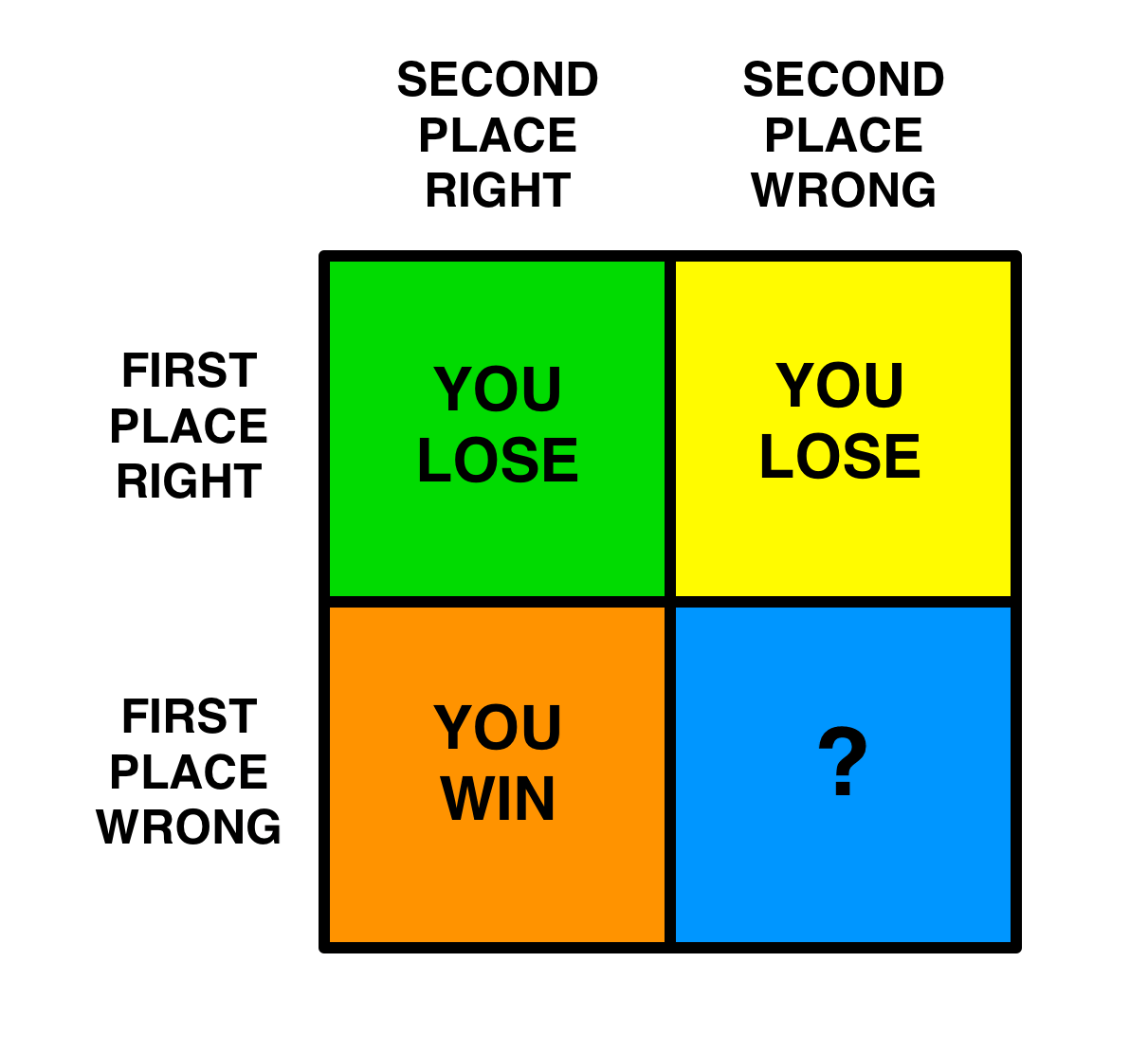
Second place, knowing that, looks at the four possibilities:
Assuming that first place will bid at least $6,001, you know in the cases where they get it right, you have no shot at winning. And in the case where they get it wrong and you get it right, they’ll have gone beneath your pre-round total trying to cover the case where you double, so you’ll win no matter what you bet.
But how about the case where you’re both wrong?
In Scenario B, first place can have their cake and eat it too, guaranteeing3 victory if they get it right (green and yellow quadrants), but also guaranteeing victory if both players get it wrong (blue quadrant). But in Scenario C, they lose their cake-eating luxury—because in order to bid enough to top second place doubling up when they both get it right, they also have bid enough that if they get it wrong, they end up below second place’s pre-round score.
This leaves the second place player with an extra little opportunity in Scenario C—knowing that first place will bid at least $6,001, they can win in the case that both players get the answer wrong by bidding little enough to stay above $3,999. That would be a $4,000 maximum bet.
 In the situation above, second place would also want to protect against third place doubling up to $6,000, so they’d bid $1,999. This would mean victory if first place got it wrong, regardless of how second or third place does on the question. A little cleverness has stolen you the blue quadrant:
In the situation above, second place would also want to protect against third place doubling up to $6,000, so they’d bid $1,999. This would mean victory if first place got it wrong, regardless of how second or third place does on the question. A little cleverness has stolen you the blue quadrant:
On Monday, James, normally beginning Final Jeopardy in first place in the automatic Scenario A or only-need-to-get-it-right Scenario B situations, found himself in a Scenario C situation—in second place—behind an extremely strong player named Emma Boettcher. This was the score:
So James did what I described above. He figured Emma would bet at least enough ($20,201) to top twice his total ($46,800) in the case that they both got the answer right.
Following that logic, he figured that if Emma got it wrong, she’d end up losing at least $20,201, bringing her down to $6,399 at most. His only shot of winning would be if Emma got it wrong, so $6,399 became his “do not cross” floor. His maximum bet would then be $17,000, which would guarantee that he beat Emma if she got it wrong, regardless of whether he got it right or not.
But like in our case above, the third-place player, Jay Sexton, was in the picture too, with $11,000. Twice Jay’s total ($22,000) became a second and higher “do not cross” line for James—so James made the perfect bet: $1,399.
With that bet, he’d win if Emma got it wrong, and Jay would have no chance of beating him—in both cases, regardless of whether he got the answer right or wrong. Being in second place isn’t a great situation to be in, but James gave himself the best shot he could.
Or did he?
See, this is where it gets interesting. James explained his reasoning in a post-show interview:
This falls in line with the traditional reasoning I laid out above. The “straight bet vs. parlay” thing is this Scenario-C–specific second place strategy I explained, where you can steal the [wrong-wrong] scenario from first place.
This is indeed how things played out. Emma bet $20,201 to cover James’s all-in bet, James correctly predicted that and bet $1,399, and both of them got it right—making Emma the winner.
But how about this part of the quote?
there was no way she wouldn’t bet to cover my all-in bet
Let’s think about this for a second. If you’re Emma, you know James is an amazing strategist who has likely analyzed every possible Final Jeopardy scenario through and through. So you can guess that he will go through the above reasoning and will therefore make a bet small enough to win in the case that you both get the answer wrong. And if he does what you expect him to, given what he assumes you’re going to do, you now have an opportunity to steal both the blue [wrong-wrong] and the orange [I’m wrong – he’s right] quadrants back from him by betting less than the traditional reasoning would tell you to.
In other words, just like James assumed “there was no way she wouldn’t bet to cover my all-in bet,” Emma could have further assumed, “there was no way James won’t assume I wouldn’t bet to cover his all-in bet.” That assumption would lead her to the conclusion that James will bet $1,399 (which he did)—which would make his maximum winnings $24,799. That’s less than her pre-round total of $26,600. So she could have guaranteed herself victory by betting nothing!
Let’s call this the Emma Mindfuck Strategy.
If you’re Emma, knowing who James is, and knowing who he thinks you are—a super smart person but still unlikely to think through this many iterations of mindfuck strategy—I believe betting nothing would have been a clever move. It’s risky, because if James doesn’t do what you think he will, you’re likely to lose. But the traditional strategy is risky for a different reason: you have to get the answer right to win. I’m not sure what the bigger risk is, but I think there’s at least a strong case for the Emma Mindfuck Strategy.
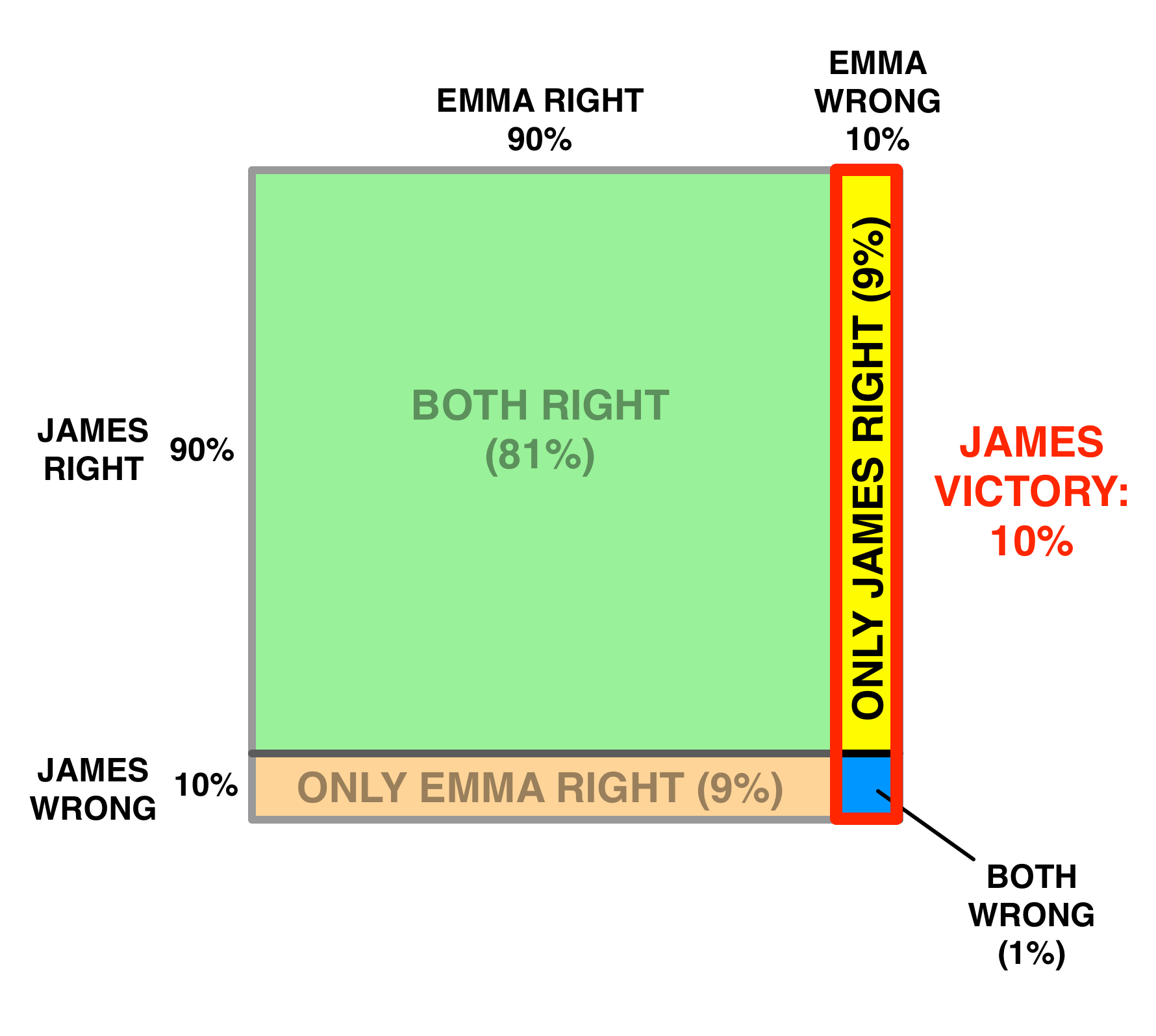
Which brings me back to James’s decision. He’s amazing at Jeopardy, and Emma clearly is too. So let’s assume that they both had a 90% chance of getting Final Jeopardy right.
That puts our four cases at these probabilities: If these probabilities are reasonably accurate, the traditional strategy James went with gave him a 10% chance of winning:
If these probabilities are reasonably accurate, the traditional strategy James went with gave him a 10% chance of winning:
 Since that’s so low, it seems reasonable to consider what I’ll call the James Double Mindfuck Strategy (JDMS).
Since that’s so low, it seems reasonable to consider what I’ll call the James Double Mindfuck Strategy (JDMS).
The JDMS thinks about the logic I laid out above that suggests there’s a strong argument for Emma to go with the Emma Mindfuck Strategy. And if Emma does go for the mindfuck, then James can hugely up his chances of winning by making a big bet instead of a small bet:
Here’s the breakdown of the four possibilities:
All James is sacrificing by opting for the JDMS instead of traditional strategy is the ability to win in the case that both he and Emma get it wrong—which is a tiny 1% sacrifice. But he gains a ton. By going with a big JDMS bet, he gives himself a 90% chance of winning if Emma goes with the mindfuck strategy herself. Sure, Emma is more likely to go with the traditional strategy—but how much more likely? Remember, on top of the general merits of the Emma Mindfuck strategy, she may also hate the clue category, which could further sway her in that direction.
For James’s traditional strategy to be the best tactic, the chances of Emma going mindfuck would have to be utterly minuscule. (It’s worth noting as well that Jay is completely irrelevant here. The only way Jay comes into the picture is if James and Emma both get it wrong and Jay gets it right—a possibility already nested within the tiny blue quadrant.)
So all things considered, I think James made the wrong decision.
Of course, if Emma has really thought things through, she’d have come upon the potential JDMS pitfall herself, which may have swayed her towards the Emma Triple Mindfuck Strategy, where she thwarts the JDMS by betting big. The fact that she did end up betting big means either that she was doing a non-mindfuck or a triple-mindfuck—whatever her reasoning was, James correctly predicted her bet and made the best bet for that prediction. But that doesn’t mean it was the right bet.
___________
Three other surprisingly short Wait But Why posts:
What Could You Buy With $241 Trillion?
___________
Add yourself to our email list and I’ll let you know when the big fat huge post is up.